The status of the pricing of the FOREX market makes comparative analysis against price movements simple.

However, this is not the case in viewing other 'averaged' financial markets like the DOW, S&P, DAX, etc.

The reason for this is the mathematics behind how those markets are priced.

If you’re trading the financial markets, you better understand this difference because otherwise you’re trying to compare an apple with a baseball....

Of note is that to this post, I have a companion video of the same title: FOREX Market Pricing Verses DOW, SP, DAX that puts all of this together from a different view point.

If you've come from watching that video, then press on here. However, if this is your starting point, I might suggest that you read through this before watching the video. Or, if you want, you can skip to the bottom of this post to watch that video now.

So, this post really is more about pricing issues in markets other than FOREX. The reason for this is because these pricing differences can cause false conclusions to be drawn about the status of those markets by un-knowledgeable people.

We don't trade FOREX in a vacuum. What's going on in all financial markets is a huge factor as to how people not only judge a country's overall economic status, but also how FOREX pair pricing is affected.

Let's use the GBP/USD pair priced at 1.3800 as an example. What exactly does that price represent?

The pair price of 1.3800 means that it's going to cost someone in the U.S. $0.38 USD more to buy something in the U.K. priced at $1.00 GBP (Pound). Conversely, someone in the U.K. changing $1.00 GBP for U.S. currency gets the U.S. product for $0.38 USD less.

The name of the pair 'GBP/USD' is actually the mathematical ratio of the value of 1 GBP to that of the USD, i.e.

GBP
---  =  1.3800
USD

 1
---  =  1.3800
USD

We can flip that around to calculate the value of 1 USD to that of GBP

GBP
---  =  1.3800
USD

1 (GBP)  =  1.3800 * USD

USD
---  =  0.7246
GBP

Make sense? The thrust of that example is to show you that the value of the GBP/USD market pair is the true and correct value of that pair with no ambiguity.

What would happen if you added up the Friday closing price of all currency pairs (there are 128 that are listed), and divided that by 128 to get the average of the FOREX market? As I'm sure you can imagine, you'd have a meaningless value because of the mix of currencies.

For example what's the average of the following 3 pairs: GBP/USD at 1.3831 US Dollars, AUD/NZD at 1.07101 New Zealand Dollars, and CHF/CZK at 23.4019 Czech Koruny? If you divide by 3, the answer is 8.6186. But what does that mean?

It means... nothing....

What you have to do is pick 1 currency like USD, and find the average of all USD quote pairs. In the case of USD, this is what's called the DXY dollar index.

DXY dollar index

The U.S. Dollar Index (USDX, DXY, DX, or, informally, the 'Dixie') is used to measure the value of the dollar against a basket of six world currencies - Euro, Swiss Franc, Japanese Yen, Canadian dollar, British pound, and Swedish Krona.

Geeky details: The U.S. dollar index is calculated by multiplying together each pairs value times a weighting factor determined by the volume of that pair within the index.

For example, GBPUSD^-0.119 (the value here of GBP/USD multiplied by its weighting factor) for the GBP/USD pair. Note that when the U.S. dollar is not the base value in the currency cross, as in the GBP/USD pairing, the value is negative.

Though that may seem pretty complicated, it creates a solid relationship between USD, for example, and all of its paired currencies. An index value for DXY of 120, for example, means that the U.S. dollar has appreciated 20% versus the basket of currencies over the time period in question.

*** For a complete discussion of these calculations see the following:

• Investopedia: What Is the U.S. Dollar Index (USDX)?
• Tradingpedia: United States Dollar Index
• Wikipedia: United States Dollar Index

The Pound GBP, for example, also has an index called BXY (British Pound Currency Index). And that makes sense because each such index is comprised of related currencies expressed in terms of the value of the quote currency.

The Dow Jones Industrial Average is one of the most prominent financial metrics in the world.

Though it is referred to as the DOW 30, meaning that there are 30 stocks in that average, this is not the case. Because of changes to the average, there are currently only 29 stocks in the DOW 30. There is an article on Investopedia (Dow 30 Is Now Dow 29 as Dow Inc. Does Not Belong' by Richard Suttmeier - Updated Jun 25, 2019) that describes when and why this happened. But regardless of that, the DOW 30 represents the most reflective and accepted status of the American economy.

And therein lies the problem: It's an average.

Yeah, so?

Well, as it turns out it's not an average. Well, more correctly: it's not a correctly computed average.

What is an average? It's a number of prices added together and then divided by the number of prices.

Let's make it easy and just look at calculating the average of 3 stocks, each priced at $30. The total is $90, and because there are just 3 stocks, then $90/3 is $30. How quaint....

Let's call my little average here the Organization Against Kryptonite 3, or OAK for short. Catchy, hu?

So, right now OAK looks like this: A = $30, B = $30, C = $30 totaling $90 with an average of $30 per share.

What is the average if C increases $1 to $31?

OAK:: A = $30, B = $30, C = $31 totaling $91 with an average of $30.33 per share.

So, by C increasing $1, the average increased by $0.33. Fair enough, but what's the point here?

Okay, what happens if all 3 companies in OAK stabilize back to $30 per share; an average of $30, but company C decides, as many companies do from time to time, that it's share price of $30 is too expensive - that folks would be more inclined to trade C if its price was to be $15.

In order to do that, C has to double the number of outstanding shares, i.e. 1, to 2 shares, each priced at $15 to equate to the current $30 stock price.

So, now OAK looks like this: A = $30, B = $30, C = $15 totaling $75 with an average of $25 per share.

Whoa! What happened to that? You can't now open the OAK market from a close yesterday at an average of $30 with an average of $25! People would scream about not have a consistently stated average that could be analyzed correctly.

Well, you did analyze it correctly: it's got an average value of $25 per share because the total value of the 3 stocks of $75 divided by those 3 stocks is... well, it's $25.

Here's the problem: what can you do with those 3 stocks such that the average will still total $30 even after the split?

This is valid to require because the split did nothing to change the capitalization of company C. Pre-split, the company had 1 share priced at a total value of $30, and after the split to $15 a share with 2 shares the company still has a capitalization or total value of $30 (2 shares at $15 = $30). None of that information can be changed.

So what could we change to make the OAK average $30 after C splits their shares? The solution equation looks like this:

First, here's the equation for averaging:

average  =  (A + B + C) / 3

And here is the data:

30  =  (30 + 30 + 15) / 3

But that does not equal 30. How about if we restate the equation with 3 being a new variable called 'divisor'....

30  =  (30 + 30 + 15) / divisor
30  =  75 / divisor
divisor  =  75 / 30
divisor  =  2.5

Whoa! There are 3 companies in OAK, so the divisor has to be 3, and not 2.5 to be a correct average. Yup.... But to make the average consistent with the previous close, the 'divisor' has to drop from 3 to 2.5.

And that's a problem.

Why?

Because, now, if the price of company C goes up $1 to $16 per share then the new 'average' becomes $76 / 2.5 which is: $30.40.

So?

So look: In OAK both examples pre-split and split have the same $1 increase. In the pre-split example, this raised the average to $30.33, but after the split the average became $30.40, or $0.07 more.

And why is this a problem?

Because nothing different happened and yet the average after split increased the value of OAK by $0.07!!!

Now, run this same logic out with 30 stocks (or 500, or 2000) with some of the higher priced stocks changing maybe $20 in a day. What do you think the result on the average value of that market will do? It's going to inflate the average tremendously!

When the DOW was established, the divisor was 30. With all of the stocks splitting over the years and prices going way up: what do you think the divisor must be now?

"As of the end of June 2018, the Dow divisor is 0.14748071991788. It means that for every $1 of change in price for any given stock within the index, the average – using the current Dow divisor – is equal to a 6.781-point movement in the market." [* Corporate Finance Institute What is the Dow Divisor?]

Let that sink in just a little: back in 2018 with the divisor at 0.14748071991788, any stock that rose $1 caused the underlying 'average' to increase by $6.78!!!!

I did some research on the DOW the other day. Adding up the values of all last closing prices came to $5,023.40 and the average of those 29 stocks is $173.22. However, the posted average is $34,501.94.

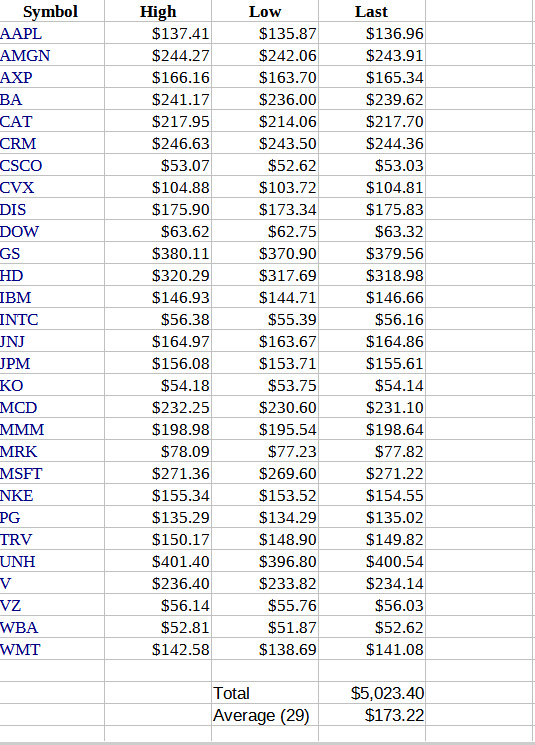
DOW 07/01/21

Terrific.... As you can see from the data I gathered for 07/01/21, the real average is $173.22 and the posted average is $34,501.94.

That makes a lot of sense, doesn't it.... If just 1 stock went up $10, it would cause the 'average' to go up about $68, and that's using the divisor from 2018!!! And that keeps skewing the average (of not only the DOW here, but any index that is an 'average', i.e. S&P, DAX, etc.

So, how do you really manage your view of what's really going on in such a market?

Beats me..... However....

The take away for us as currency traders is to be aware that any 'averaged' financial market where instruments can be split or otherwise manipulated where the divisor needs to be 'adjusted' in order to keep the published 'average' consistent creates a magnified average as opposed to the FOREX market which has none of that shading. In FOREX, the price is the price, and any average of those prices is a true average.

Video: FOREX Market Pricing Verses DOW, SP, DAX